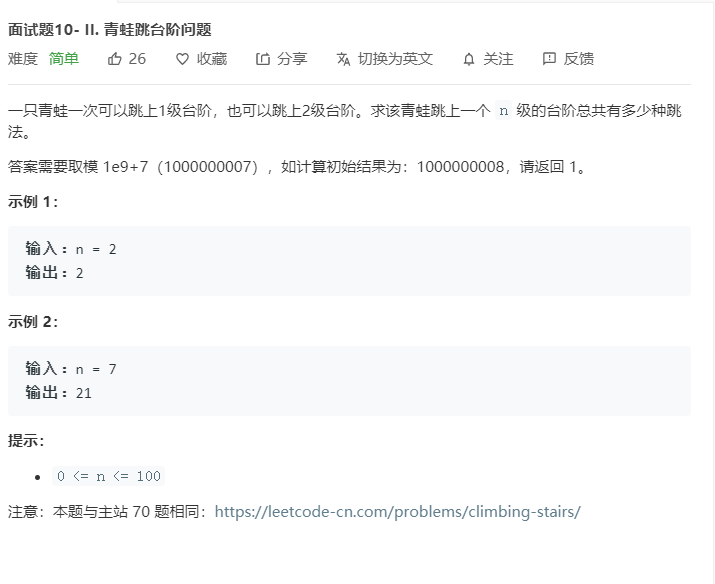
题目

题解

这题与70题一样，详见70题题解，因为要取模，因此通项公式法无法通过，递推公式法也太慢通过不了，其分析详见70题题解，这里贴一个递推公式法

其实也可以用一个dp数组存每个位置的数，但是没必要，每个位置的数只与前两位有关，用两个变量存前两个数并实时更新。再注意一下0，1，2位的特殊情况就好
本题还要注意取模，且必须每次运算完取模，若最后取模会溢出
注意这里与斐波那契数列问题的区别，

  1. 从1开始，因此n=0时返回1
  2. 也因为从1开始，因此要计算到第n个数，i<n+1（上一题是从0开始，计算到n-1）
  • 时间复杂度$O(n)$
  • 空间复杂度$O(1)$
class Solution {
public:
    int numWays(int n) {
        if(n==0) return 1;//特殊情况
        int a=1, b=1;//设置前两位
        int c = 0;
        for(int i=2; i<n+1; ++i){
            c = (a + b)%(int)(1e9+7);
            a = b;
            b = c;
        }//递推
        return b;
    }
};